[最も人気のある！] x^2 y^2 z^2-xy-yz-zx is always positive 899445

The Roman surface or Steiner surface is a selfintersecting mapping of the real projective plane into threedimensional space, with an unusually high degree of symmetryThis mapping is not an immersion of the projective plane;X2y=8 graphically and find the coordinates of the points where corresponding lines intersect y Explanation Making m = x −y n = y −z p = x −z we have m2 n2 p2 = 2(x2 y2 z2 − x ⋅ y − x ⋅ z −y ⋅ z) then x2 y2 z2 −x ⋅ y − x ⋅ z − y ⋅ z = 1 2((x − y)2 (y − z)2 (x −z)2)

Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive Brainly In

X^2 y^2 z^2-xy-yz-zx is always positive

X^2 y^2 z^2-xy-yz-zx is always positive-Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreHere is a video to illustrate about Inequality and Fraction

Suppose That X Y And Z Are Positive Integers Such That Xy 6 Xz 10 And Yz 15 What Is The Value Of Xyz Quora

X 2 y 2 z 2 xy yz zx is always positive Share with your friends Share 0 Dear Student, Please find below the solution to the asked query We have x 2 Now we multiply by in whole equation and get 2 ( x 2 y 2 z 2 xy yz zx ) Prove that x^2y^2z^2xyyzzx is always positive Please answer as fast as you can 1 See answer cutiepie is waiting for your help Add your answer and earn points60/x^2=15 x^2=60/15 x^2=4 x=2 step3 substitute for the value of x in the first two equations to find the value of y and z 2y=6 y=3 2z=10 z=5 The answer is x=2, y=3, z=5 If you are looking for the multiplication of xyz then the answer would be 2*3*5=30

Prove that x2 y2 z2 xyyzzx is always positive Solve the system of equations 2xy=1;Note that if \omega is a complex cube root of unity, then x^2y^2z^2 xy yz zx = (xy\omega z\omega^2)(xy\omega^2 z\omega) Thus it is sufficient to prove that xy\omega z\omega^2 Note that if ω is a complex cube root of unity, then x 2 y 2 z 2 − x y − y z − z x = ( x y ω z ω 2 ) ( x y ω 2 z ω ) Thus it is sufficient to prove that x y ω z ω 2(2x 5), log3 (2x 7/2) are in arithmetic progression, then the value of x is equal to Cevap 3 Show answer Math, Write down the following fractions with same least denominators first 1 by 2, 2 by 3, 3 by 4, 4 by 5

 To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW factorise `x,y,z,x^2,y^2,z^2,yz,zx,xy`Click here👆to get an answer to your question ️ If xy yz zx = 1, prove that x1 x^2 y1 y^2 z1 z^2 = 4xyz (1 x^2 ) (1 y^2 ) (1 z^2 ) x^2y^2xzyz=(xy)(xyz) x^2y^2xzyz =(x^2y^2)(xzyz) =(xy)(xy)(xy)z =(xy)((xy)z) =(xy)(xyz) Note the step where we replace (x^2y^2) with (xy)(xy

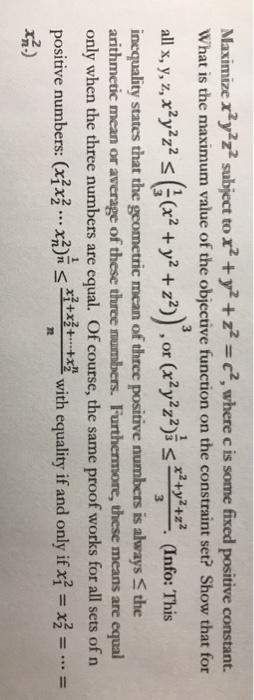
Maximize Xy Z Subject To X2 Y2 Z2 C Where C Chegg Com

Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube

X^2y^2z^2xyyzzx =(1/2)(2x^22y^2 2z^22xy2yz2zx) =(1/2)(xy)^2(yz)^2(zx)^2 =a positive quantity Thats allSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Consider A Data Set Consisting Of Values For Three Chegg Com

X 2 Y 2 Z 2 X Y Y Z Z X Is Always Positive

Contact Pro Premium Expert Support »X 2 y 2 z 2 xy yz zx = 2(x 2 y 2 z 2 xy yz zx) = 2x 2 2y 2 2z 2 2xy 2yz 2zx = x 2 x 2 y 2 y 2 z 2 z 2 2xy 2yz 2zx = (x 2 y 2 2xy) (z 2 x 2 2zx) (y 2 z 2 2yz) = (x y) 2 (z x) 2 (y z) 2 Since square of any number is positive, the given equation is always positive 5 If x, y, z ∈ R and x y z = 4 and x2 y2 z2 = 6, Then range of xyz MyTry Using (x y z)2 = x2 y2 z2 2(xy yz zx) So we get 16 = 6 2(xy yz zx) ⇒ xy yz zx = − 5 and given x y z = 4 Now let xyz = c, Now leyt t = x, y, z be the roots of cubic equation, Then (t − x)(t − y)(t − z) = 0 ⇒ t3 − (x

13 Using Properties Of Determinant Prove That Y2 Z2 Z Z Scholr

2

 Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange Would the solution be something like \begin{align*} x^2 &>y^2 \\ xx&>yy\\ \sqrt{xx}&>\sqrt{yy}\\ x&>y \end{align*} I feel like I'm not proving something though Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share theirHence, at least one among x^2, y^2 and z^2 is divisible by 3 (by 9 actually, but we don't need that) If we consider the case when both x^2 and y^2 have a remainder 1 when divided by 3, then z^2 will have a remainder 2 when divided by 3 which is not possible So we have to prove that xyz=5p All squares give remainders 0,1 or 4 when divided by 5

Factorise Xy Z 2 1 Z X 2 Y 2 Lalajveer

Show That The Equation X 2 Y 2 Z 2 X Y Y Z Z X Has Infinitely Many Solutions In Integers X Y Z M Cube Mathematics By Maheshwari

 0 Office_Shredder said (xy) 2 = x 2 2xy y 2 >= 0 You know that already So x 2 xy y 2 >= xy If x and y are both positive, the result is trivial If x and y are both negative, the result is also trivial (in both cases, each term in the summation is positive) When one of x or y is negative, xy becomes positiveAnalyzing quadratic forms x^23xyy^2, 2xyyz3xz and x^2y^22xyxt2yt Positive, negative or indefinite?Analyzing quadratic forms x 2 − 3 x y y 2 , 2 x y y z − 3 x z and x 2 y 2 2 x y − x t

Divergence Theorem Example 1 Video Khan Academy

If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Youtube

= (x 2 y 2 2xy) (z 2 x 2 2zx) (y 2 z 2 2yz) = (x y) 2 (z x) 2 (y z) 2 Since square of any number is positive, the given equation is always positiveIs always positive Answers 3 Show answers Another question on Math Math, 00 If log3 2, log; Click here👆to get an answer to your question ️ Show that x^2 xy y^2, z^2 zx x^2 and y^2 yz z^2 are consecutive terms of an AP, if x, y and z are in APDivide y, the coefficient of the x term, by 2 to get \frac{y}{2} Then add the square of \frac{y}{2} to both sides of the equation This step makes the left hand side of the equation a perfect squareShare It On Facebook Twitter Email

Prove That X Y Z Xy Yz Zx Is Always Positive Brainly In

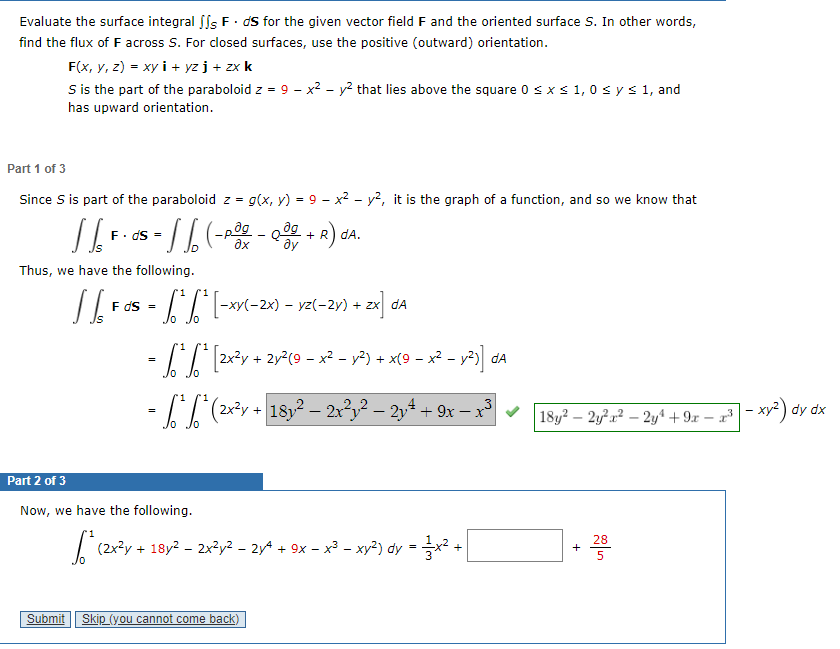
Evaluate The Surface Integral S F Ds For The Given Chegg Com

 Theorem The positive primitive solutions of x^2 y^2 = z^2 with y even are x = r^2 s^2, y = 2rs, z = r^2 s^2, where r and s are arbitrary integers of opposite parity with r>s>0 and gcd(r,s)=1 Using this theorem, find all solutions of the equation x^2 y^2 = 2z^2 (hint write the x^2y^2z^2=xyyzzx eq(1) Identity is x^3y^3z^3 3xyz=(xyz)(x^2y^2z^2xyyzzx) x^3y^3z^3 3xyz =(xyz)(xyyzzxxyyzzx) (acc to eq1) Therefore , x^3y^3z^3 3xyz = 0 So, x^3y^3z^3= 3xyz Answer read more (x – y)2 (y – z)2 (z – x)2 , This expression is the sum of three perfect square numbers and it is not possible to make this expression less than 0 Correct Option 10 Best Solution (5) Anantha Krishna 11 years AGO if x=y=z, then the equation becomes 0, in all other cases it will be more than 0 So it is not possible

If X2 Y2 Z2 1 Then Xy Yz Zx Lies In The Interval

Is 8 X 3 Y 3 Z 3 2 Ge 9 X 2 Yz Y 2 Xz Z 2 Xy True For Nonnegative Numbers Mathematics Stack Exchange

X^2y^2z^2=1 WolframAlpha Have a question about using WolframAlpha?Correct answer to the question Prove that x² y² z² xy yz zx is always positive brainsanswersincomAnswer 2 on a question Prove that x^2y^2z^2xyyzzx is always positivePlease answer as fast as you can the answers to answersincom

Q Tbn And9gcsvmufbiw2 Akbfcnfzd7krkct6uxai55t1 B E H4p5qap22fm Usqp Cau

X 2 Y 2 Z 2 Xy Yz Zx Is Always Positive Brainly In

QA>A cyclist goes 40 km towards East and then turning to right he goes 40 km Again he turn to his left and goes km After this he turns to his left and goes 40 km, 4 Let x, y, z > 0 satisfy xy yz zx 2xyz = 1 Prove that 4x y z ≥ 2 The condition invites the factoring (1 x)(1 y)(1 z) xyz − 2 = x y z, but having the factor 4 in the desired inequality makes things more difficult algebraprecalculus inequality ShareSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Rd Sharma Solutions For Class 8 Chapter 1 Rational Numbers Exercise 1 6 Avail Free Pdf

Cms Math Ca Concours Mocp 00 Sol Sep Pdf

But a national level competition always require a pure mathematical proof These are all solutions with $$ 2 \leq x < y < z < 1700 $$ For some reason there are just a few solutions with some positive entries and some negative, that probably has a short proof once all three are positive and distinct, it is easy to see that we canProve that x 2 y 2 z 2 xy yz zx is always positive for distinct values of x, y and z Share with your friends Share 2 Dear Student, Please find below the solution to the asked query We have x 2 y 2 z 2 xy yz zy Now we multiply by in whole equation and get 2 ( x 2 y 2 z 2 xy yz  answers K people helped Answer Hello We have x2 y2 z2 xy yz zy and we have to prove that it is always positive Now we multiply the whole equation by 2 and get 2 ( x² y² z² xy yz zx ) ⇒2x² 2y² 2z² 2xy 2yz 2zx ⇒ x² x² y² y² z² z² 2xy

If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora

If X Y Z Are Positive Integers Then Value Of The Expression X Y Y Z Z X Is A 8xyz B 8xyz C 8xyz D 4xyz Dronstudy Questions

However, the figure resulting from removing six singular points is one Its name arises because it was discovered by Jakob Steiner when he was in Rome in 1844Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor And by "clever manipulations," Arildno means group the x 2, xy, and y 2 terms together, and group the x 2, xz, and z 2 terms together, and group the y 2, yz, and z 2 terms together It's possible that some factorization can occur #5 Elucidus 286 0

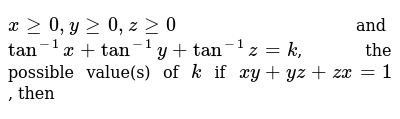
Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive

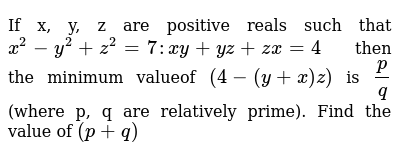
If X Y Z Are Positive Reals Such That X 2 Y 2 Z 2 7 Xy

Write x^2y^0z^2/xy using only positive exponents Questions in other subjects Mathematics, 30 Two sides of a right triangle are 8 and 12 find the hypotenuse Answers Mathematics, 30 Find the base of the triangle whose area is 24 cm² and who is height is 16 cmCorrect answer to the question Prove that x^2 y^2 z^2 xy yz – zx is always positive elearningincom If x y z = 0, then \(\frac{x^2}{2x^2yz}\frac{y^2}{2y^2zx}\frac{z^2}{2z^2xy}\) = (a) 4 (b) 2 (c) 3 (d) 1 Login Remember

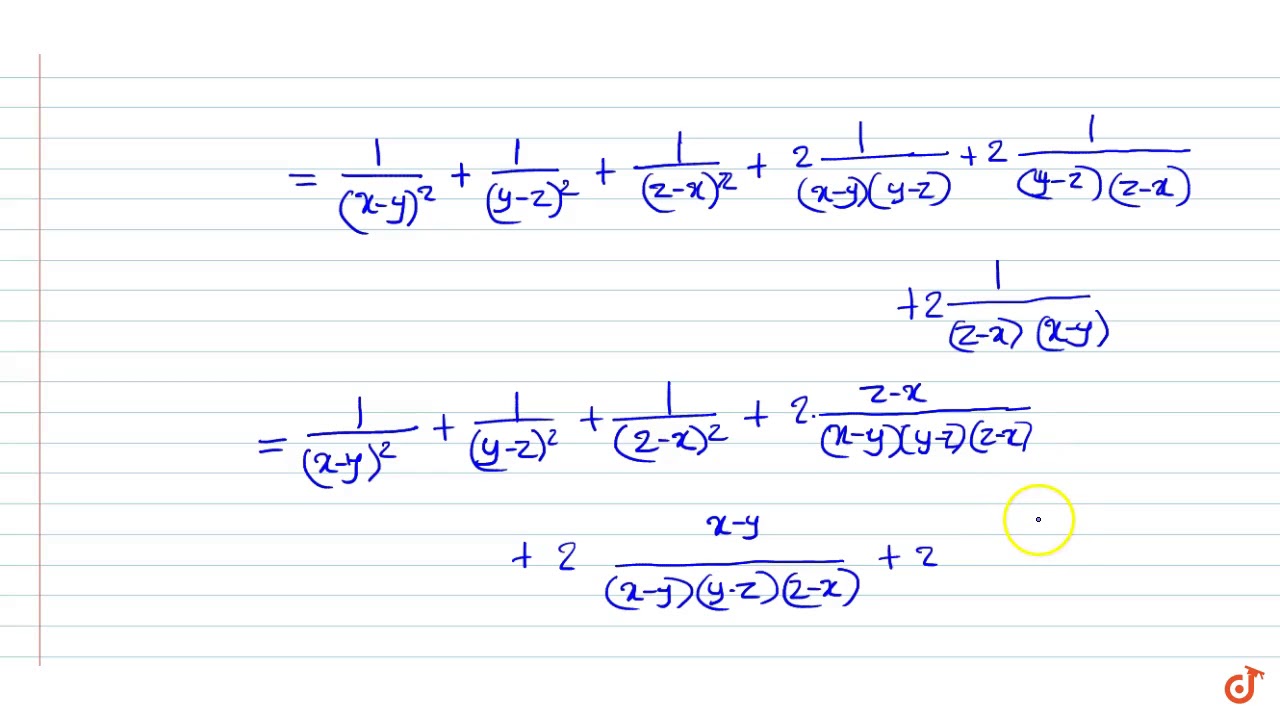
If X Y Z Are All Different Real Numbers Then Prove That 1 X Y 2 1 Y Z 2 1 Z X 2 Youtube

Xy Yz Zx 1 Then The Expression X Y 1 Xy Y Z 1 Yz Z X 1 Zx Is Equal To Brainly In

How To Do Implicit Differentiation 7 Steps With Pictures

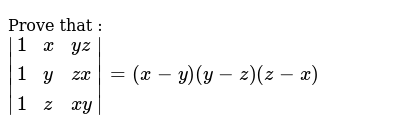
Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive

Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive

Users Math Msu Edu Users Maccomb1 Ss15 234 Ch16 Ch16 Filled Pdf

X2 Y2 Z2 24 Nd Xy Yz Zx Find X Y Z Brainly In

X2y2z2 Xy Yz Zx Is Always Pos See How To Solve It At Qanda

Prove That X 2 Y 2 Z 2 Xy Yz Zx Is Always Positive Brainly In

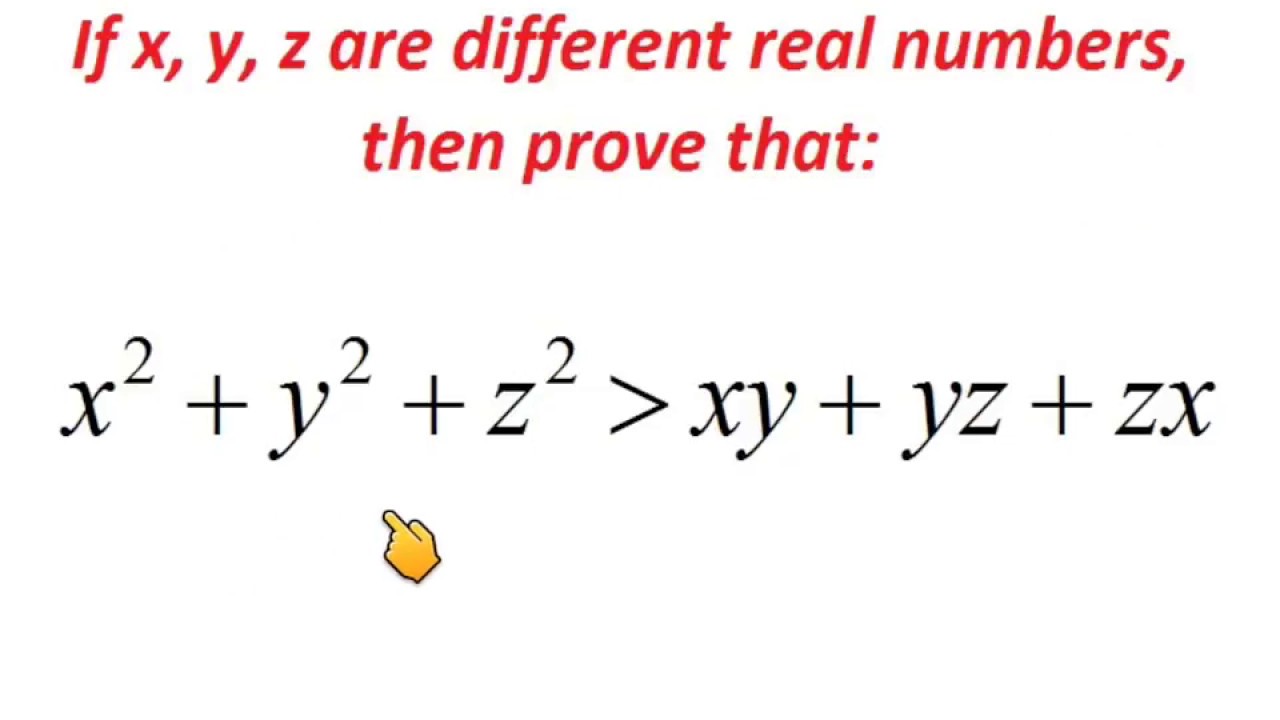
X 2 Y 2 Z 2 Greater Than Xy Yz Xz Proof Important For Iit Jee Nda Scra Sat Competitive Exams Youtube

9 1 Matrix Of A Quad Form

If Xy Yz Zx 1 Show That X 1 X 2 Y 1 Y 2 Z 1 Z 2 4xyz

1

Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive Brainly In

How To Prove That Math X 2 Y 2 Z 2 Xy Yz Zx Math Is Always Positive Quora

X2y2z2 Xy Yz Zx Is Always Pos See How To Solve It At Qanda

Find The Directional Derivative Of F X Y Z Xy Yz Chegg Com

Quadratic Function Wikipedia

Http Webpages Fc Ul Pt Jaruiz Multivariable Calculus Excerptsmath23b Pdf

Selina Solutions Class 9 Concise Maths Chapter 4 Expansions Download Free Pdf

Factorise X2 Y2 Z2 Xy Yz Zx X 2 Y 2 Z 2 Xy Yz Zx Factors Of B2 C2 Ab Ca Youtube

Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf

Prove That X Sq Y Sq Z Sq Xy Yz Zx Is Always Positive Brainly In

4 Partial Derivatives And Their Applications Derivative Variable Mathematics

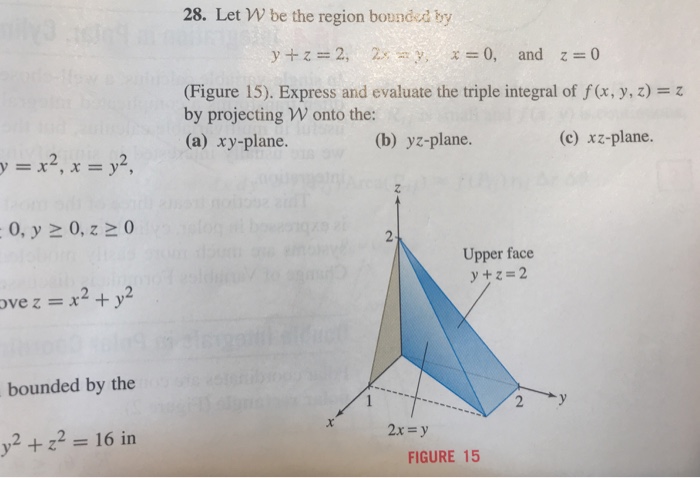
28 Let W Be The Region Bounded By Y Z 2 2x Y X 0 Chegg Com

Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf

Please Do It Using Identities Prove That X Y 3 Xy Yz Zx Where X Y Z Maths Lines And Angles Meritnation Com

The X Y Y Z Z X And Stereo Views Of The Architected 3d Chiral Download Scientific Diagram

Link Springer Com Content Pdf 10 1007 Bf Pdf

Prove That X Y Z Xy Yz Zx Is Always Positive Mathematics Topperlearning Com 58pxibcc

Suppose That X Y And Z Are Positive Integers Such That Xy 6 Xz 10 And Yz 15 What Is The Value Of Xyz Quora

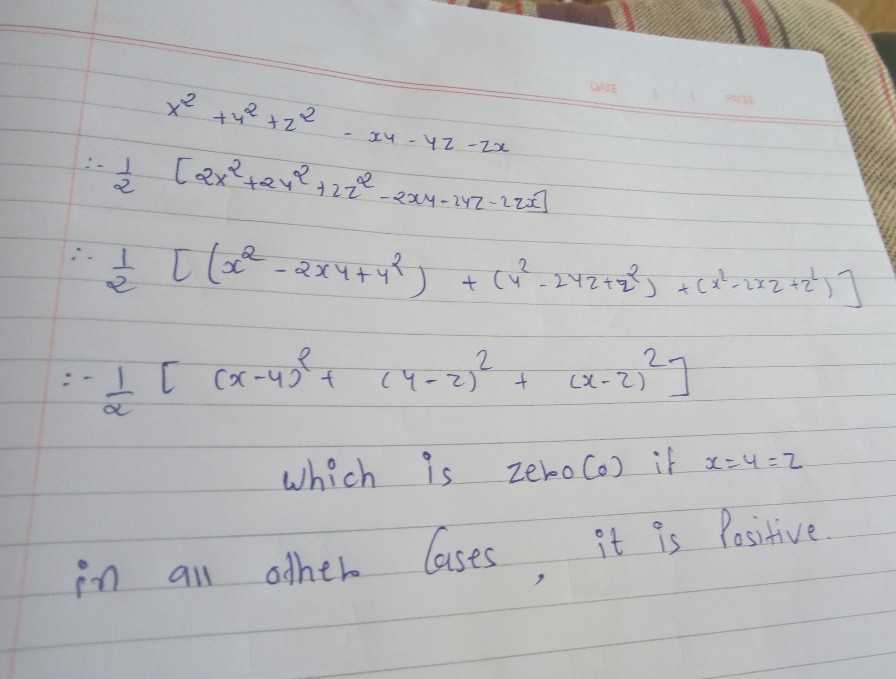
Prove That X 2 Y 2 Z 2 Xy Yz Zx Is Always Positive Scholr

How To Prove That Math X 2 Y 2 Z 2 Xy Yz Zx Math Is Always Positive Quora

Prove That X Y Z Xy Yz Zx Is Always Positive Brainly In

2

How To Prove That Math X 2 Y 2 Z 2 Xy Yz Zx Math Is Always Positive Quora

Prove That 1x2 Y2 Z2 Xy Yz Zx Is Always Positive Scholr

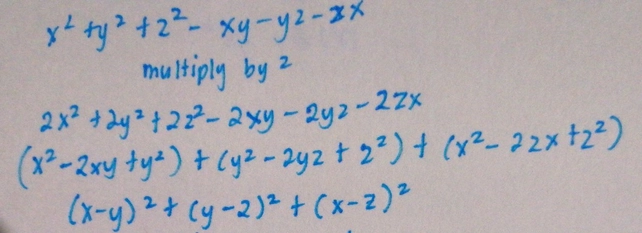
Prove That X2y2z2 Xy Yz Zx Is See How To Solve It At Qanda

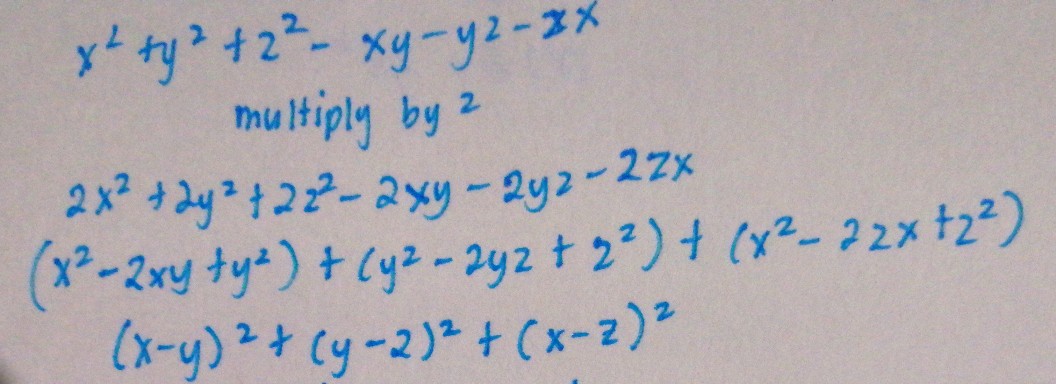
Prove That X2y2z2 Xy Yz Zx Is See How To Solve It At Qanda

Use Stokes Theorem To Evaluate 3 Curl F Ds Chegg Com

10 If X Y And Z Are Three Different Numbers Theprove That X2 Y2 Z2 Xy Yz Zx Is Always Brainly In

Homework 8 Model Solution Han

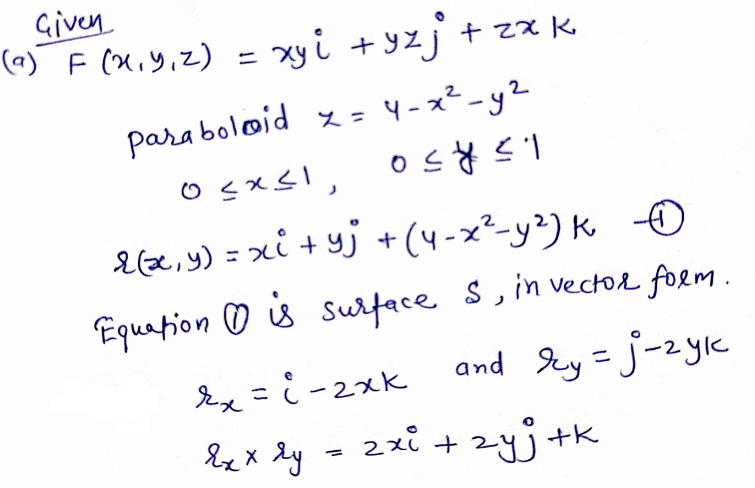
Answered Evaluate The Surface Integral Sf Bartleby

X2y2z2 Xy Yz Zx Is Always Pos See How To Solve It At Qanda

Search Q X3 2by3 2bz3 3xyz Tbm Isch

Mr Year 14 Problem Column Pdf Triangle Square Root

What Is The Way To Factorize X 2 Y 2 Z 2 Xy Yz Zx Quora

Update Ans Prove That X 2 Y 2 Z 2 Xy Yz Zx Always Positive

The X Y Y Z Z X And Stereo Views Of The Architected 3d Chiral Download Scientific Diagram

If X Y And Z Are Real Numbers Such That X Y Z 1 Then What Is The Value Of Xy Yz Xz Quora

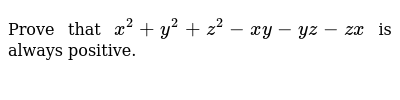
Prove That X 2 Y 2 Z 2 X Y Y Z Z X Is Always Positive

Evaluate The Surface Integral F Ds For The Given Chegg Com

If X Y And Z Are Real And Different And U X 2 4 Y 2 9 Z 2 6 Y Z 3 Z X 2 X Y Then U Is Always A Non Negative

X2y2z2 Xy Yz Zx Is Always Pos See How To Solve It At Qanda

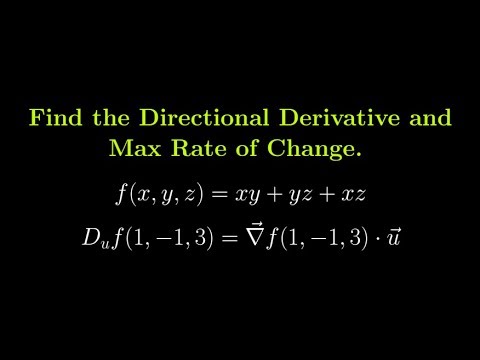
Find The Directional Derivative Of F X Y Z Xy Yz Xz At 1 1 3 In The Direction Of 2 4 5 Youtube

Users Math Msu Edu Users Maccomb1 Ss15 234 Ch16 Ch16 Filled Pdf

The X Y Y Z Z X And Stereo Views Of The Architected 3d Chiral Download Scientific Diagram

Users Math Msu Edu Users Gnagy Teaching 10 Fall Mth234 W14 234 H Pdf

Search Q X2 2by2 2bz2 Formula Tbm Isch

How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange

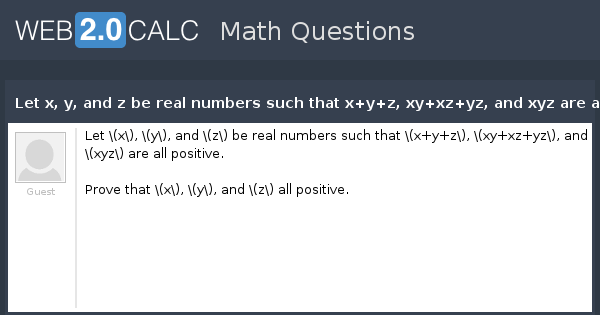
View Question Let X Y And Z Be Real Numbers Such That X Y Z Xy Xz Yz And Xyz Are All Positive

Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive

Factorise Xy Z 2 1 Z X 2 Y 2 Lalajveer

Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive Brainly In

X2y2z2 Xy Yz Zx Is Always Pos See How To Solve It At Qanda

Www Shaalaa Com Question Bank Solutions Prove That X2 Y2 Z2 Xy Yz Zx Is Always Positive Special Product

Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf

If X Y Z 1 X Y Y Z Z X 1 And X Y Z 1 Find The Value Of X 3 Y 3 Z 3dot Youtube

Www Amherst Edu System Files Solution 25practice 25test 253 0 Pdf

If Math X 2 Y 2 Z 2 Xy Yz Zx 0 Math How Can I Prove That X Y Z Quora

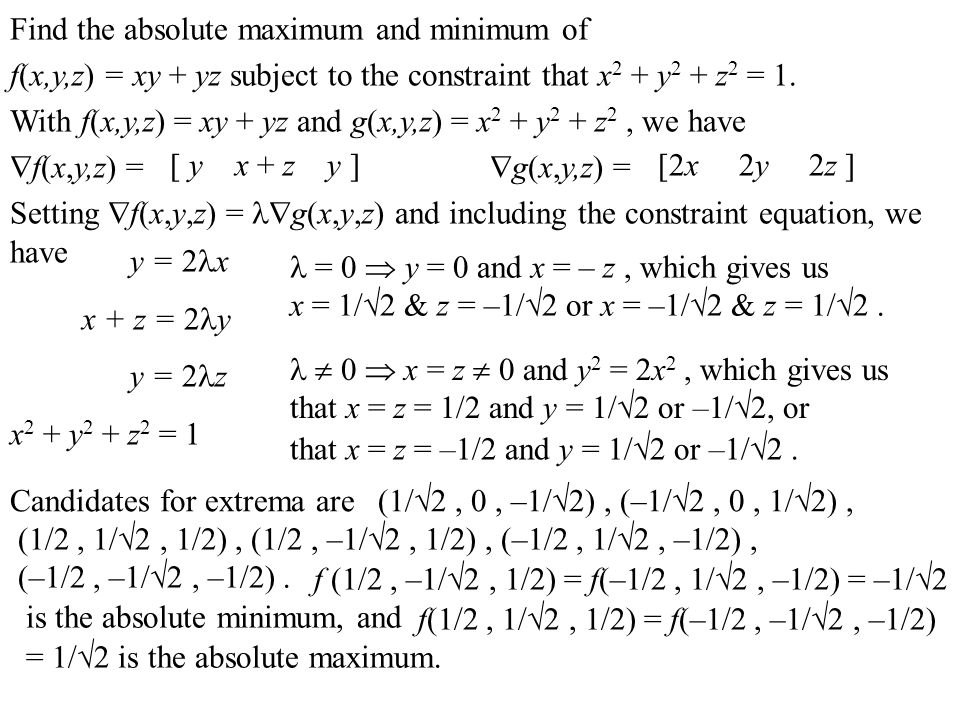
Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download

Pdf Extrema Of Xy Yz Zx When X Y Z And Xyz Are Constant

Webwork Exam Review Solutions

What Is The Way To Factorize X 2 Y 2 Z 2 Xy Yz Zx Quora

Users Math Msu Edu Users Maccomb1 Ss15 234 Ch16 Ch16 Filled Pdf

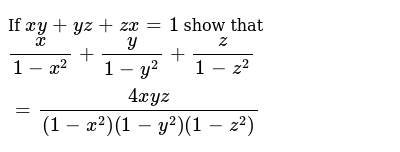
If Xy Yz Zx 1 Show That X 1 X 2 Y 1 Y 2 Z 1 Z 2 4xyz

Projecteuclid Org Journals Experimental Mathematics Volume 9 Issue 1 On The Representations Of Xyyzzx Em Pdf

X2y2z2 Xy Yz Zx Is Always Pos See How To Solve It At Qanda

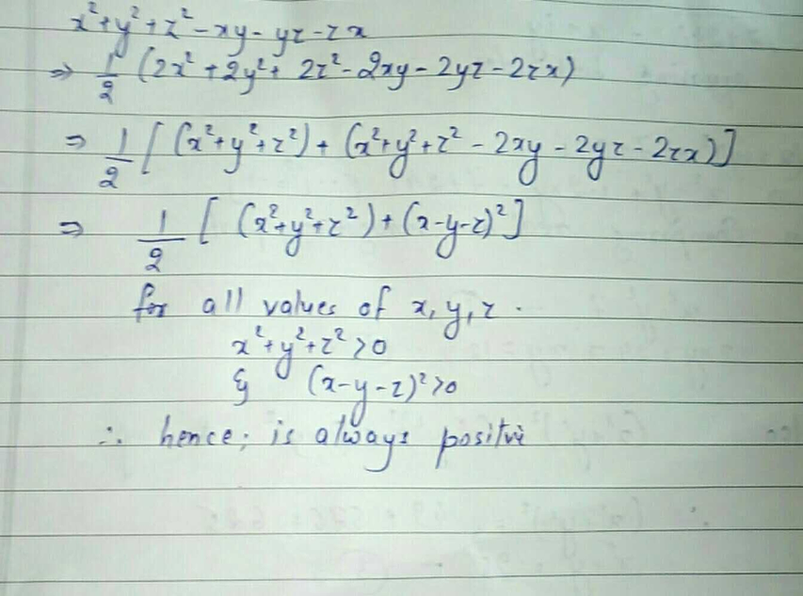
Prove That 1x2 Y2 Z2 Xy Yz Zx Is Always Positive Scholr

10 Prove That X2 Y2 Z2 Xy Yz Zx Is Always Posit Scholr

X 2 Y 2 Z 2

Www Math Ucla Edu Mt 131a 1 02s 131a Hw Sol Pdf